-
Gregory Nagy, Comparative Studies in Greek and Indic Meter
Foreword
Acknowledgments
Checklist of Greek (G) and Indic (I) Metrical Terminology
Symbols
Abbreviations of Editions
Introduction
Part I. κλέοc ἄφθιτον and Greek Meter
1. The Common Heritage of Greek and Indic Meter: A Survey 2. Internal Expansion 3. On the Origins of Dactylic Hexameter 4. The Metrical Context of κλέοc ἄφθιτον in Epic and Lyric 5. The Wedding of Hektor and Andromache: Epic Contacts in Sappho 44LP 6. Formula and Meter: A Summary Part II. śráva(s) ákṣitam and Indic Meter
7. The Metrical Context of Rig-Vedic śráva(s) ákṣitam and ákṣiti śrávas 8. An Inquiry into the Origins of Indic Trimeter 9. The Distribution of Rig-Vedic śrávas: An Intensive Correlation of Phraseology with Meter Epilogue: The Hidden Meaning of κλέοc ἄφθιτον and śráva(s) ákṣitam Appendix A. μήδεα and ἄφθιτα μήδεα εἰδώc Appendix B. Dovetailing: Speculations on Mechanics and Origins Selected Bibliography
3. On the Origins of Dactylic Hexameter
I propose that the archetype of the dactylic hexameter is the pattern pher3d, as it is still used by Alkaios: [1]
1̄̆ 2̄̆ 3̄ 4̆ 5̆ 6̄ 7̆ 8̆ 9̄ 10̆ 11̆ 12̄ 13̆ 14̆ 15̄ 16̄̆
This proposal entails that the original hexameter must have operated on an inherited principle of isosyllabism (as still maintained by Alkaios). Since a pher3d consists of 16 syllables, this conjectured prototype of Greek epic verse matches the syllable-count of the śloka, the basic unit of Indic epic versification. (By origin, the śloka is composed of two 8-syllable Anuṣṭubh verses.)In order to derive the dactylic hexameter from pher3d, I postulate the following developments in pher3d: (1) the optional replacement of – ⏑ ⏑ by – –; (2) the replacement of ⏓ ⏓ by – –, which is optionally replaced by – ⏑ ⏑. Let us first examine how the equation of two shorts (in – ⏑ ⏑) with one long (in – –) may have come about. Possibly, it is the reflex of a dramatic change in the Greek language, namely, the contraction of vowels after the disappearance of intervocalic *s and *y. Imagine that, where V = ‘vowel’, the original patterns *… V̆1sV̆2 … and *… V̆1yV̆2 … of certain words in certain formulas become … V̄3 … in the natural language. In that case, the formulas that contained {49|50} these words set the precedent for two shorts equaling one long within their metrical framework. Then the equation ‘two shorts equal one long’ may become extended beyond the original confines of the formulas that generated it, so that new formulas with spondee (– –) instead of dactyl (– ⏑ ⏑) are admitted to epic hexameter. In another work, [2] I have elaborated on such metrical phenomena to the extent of drawing up an axiom. We might say that traditional meter and traditional phraseology are formally correlate in origin. If a formal change occurs within the phraseology, it may trigger a corresponding change in the meter. Thus formulas may set new precedents for meter, which may then accommodate new formulas.
Whatever the linguistic origins of substituting spondees for dactyls, it is possible to demonstrate from the internal evidence of epic hexameter that in certain respects the spondee is alien to the 2nd, 3rd, 4th, 5th feet but not alien to the 1st. Unlike dactyls, spondees generally cannot be followed by a word-break in any foot except the 1st (and of course the 6th). Such a constraint against spondees implies that they may not be basic to the 2nd, 3rd, 4th, 5th feet; conversely, the absence of this constraint at the 1st foot implies that the spondee may be basic there. Thus the current dynamics of epic hexameter allow for at least the possibility of {50|51} a pher3d prototype:
| 1̄̆ 2̄̆ | 3̄ 4̆ 5̆ | 6̄ 7̆ 8̆ | 9̄ 10̆ 11̆ | 12̄ 13̆ 14̆ | 15̄ 16̄̆ |
| 1st | 2nd | 3rd | 4th | 5th | 6th feet |
We are left with serious problems, however. Why, for example, should 1̄̆ 2̄̆ be gradually replaced by 1̄ 2̄ (and 1̄ 2̆ 2̆½)? Also, what was the internal cause for any constraint against word-breaks after spondees? For answers we may find it useful to examine Allen’s theory of ictus. Even before we begin such an examination, however, I should note that Allen’s theory is not indispensable for my own theory of pher3d origins for the hexameter. It is, however, at the very least, a useful point of departure.
According to Allen, ictus in Greek verse is a direct reflex of stress in the Greek language. [3] The Greek stress-system was originally independent of the Greek intonation-system, the patterns of which are well known from the Attic and Ionic evidence. (For example, we learn that proparoxytone becomes paroxytone when the ultimate vowel is long.) By contrast with the manifold rules for {51|52} intonation, two will suffice for stress. Allen’s formulation is as follows: “(a) words were primarily stressed on their last heavy syllable [monosyllabic words generally do not count, since they afford no opportunity for contrast of stress within the word]; (b) a secondary stress fell on preceding heavy syllables if separated from the primary stress by at least one mora of quantity.” [4] (The dots underneath syllables will henceforth indicate stress.) For example,
ἄ̣νδρα μοι ἔ̣ννεπε Μο̣ῦcα πολύ̣τροπον ὃ̣c μάλα πο̣λλά
(Odyssey α 1)
ὦ κο̣ινὸν α̣ὐτάδε̣λφον ʼΙ̣cμήνη̣c κάρᾶ̣.
(Sophokles Antigone 1)
The testing of this formula on vast numbers of dactylic hexameters and iambic trimeters led Allen to his theory that ictus in Greek verse coincides with stress in the Greek language. [5] Clearly, the dictum applies: the dynamics of {52|53} poetic language, whether or not they are still dependent on the natural language, nevertheless originate from the actual grammatical rules of the latter. [6] We must take note of an elusive but important implication in these two stress-rules: a given word such as one ending in -οc will have two different stress-patterns, depending on whether the next word begins with a vowel or consonant. The pattern -οc V- lacks ictus, vs. the pattern -ο̣c C-, with ictus. When a pause follows the final syllable of a word, stress is indifferent and subject to determination by the preceding rhythm. [7]
From the synchronic point of view, the dactylic hexameter displays the following patterns of ictus:
–̣ ⏔ –̣ ⏔ –̣ || ⏔ –̣ ⏔ –̣ ⏔ –̣ ⏓ (with penthemimeral caesura)
–̣ ⏔ –̣ ⏔ –̣ ⏑ || ⏑ –̣ ⏔ –̣ ⏔ –̣ ⏓ (with trochaic caesura)
–̣ ⏔ –̣ ⏔ –̣ ⏔ –̣ || ⏔ –̣ ⏔ –̣ ⏓ (with hephthemimeral caesura) {53|54}
–̣ ⏔ –̣ ⏔ –̣ ⏑ || ⏑ –̣ ⏔ –̣ ⏔ –̣ ⏓ (with trochaic caesura)
–̣ ⏔ –̣ ⏔ –̣ ⏔ –̣ || ⏔ –̣ ⏔ –̣ ⏓ (with hephthemimeral caesura) {53|54}
(The verse-final arrangement is –̣ ⏓, not – ⏓̣, in accordance with the preceding pattern of descending rhythm.) [8] All major types of word-break have been indicated here, except for one:
–̣ ⏔ –̣ ⏔ –̣ ⏔ –̣ ⏑ ⏑ || –̣ ⏔ –̣ ⏓ (with bucolic diaeresis)
At this point, we must add a modification based on Allen’s theory: whereas the verse-final pattern –̣ ⏑ ⏑ || –̣ ⏔ –̣ ⏓ conforms to the ictus-rhythm, any corresponding spondaic type – –̣ || –̣ ⏔ – ⏓ upsets ictus-rhythm. The ictus in this instance is forced into the second part of the foot. Accordingly, of plurisyllabic Homeric words with heavysyllable final, only about 7% end with the 4th foot, as opposed to over 50% of plurisyllabic words ending in a dactyl. [9] As for the 5th foot, the apparent innovation of substituting a long for two shorts has had the least effect—a sign of archaism that we might expect from the ending of the verse. But even in the 5th foot, the spondaic incursion is significant enough to leave one spondee for every twenty dactyls. By contrast, a spondaic-final word that ends with the 5th foot is practically nonexistent, with only three certain instances in the whole Homeric corpus. [10] In the 2nd foot as well, the frequency of spondaic word-ending is extremely low: of plurisyllabic words with heavy final, only about 2.6% end with the 2nd foot—this despite the {54|55} fact that spondees are even more common in the 2nd foot than in the 4th. [11] In sum, spondees may occur in every foot of the hexameter, but spondaic word-endings cannot normally coincide with foot-endings. According to Allen’s theory, this constraint helps avoid disruption of the ictus-rhythm in the verse.The one exception is the 1st foot. Although spondees are only very slightly more common here than in the 4th foot, spondaic word-endings are three times more common; in fact, there is a spondaic word-ending in the 1st foot once in every 10 lines. [12] These facts suggest that the 1st foot of the epic hexameter is not by origin a dactyl (– ⏑ ⏑) but a spondee (– –). Here, in terms of my theory, the equation of – ⏑ ⏑ with – – was operative in the reverse order: from spondee to dactyl, not dactyl to spondee as in the 2nd, 3rd, 4th, 5th feet. The spondee of the 1st foot can in turn be traced back to the Aeolic base (⏓ ⏓), which internal lyric evidence shows being gradually restricted to – – and – ⏑ in preference to ⏑ – and ⏑ ⏑. [13]
I return to my reconstruction of the epic hexameter as the archetypal pattern pher3d still preserved by Alkaios: [14]
1̄̆ 2̄̆ 3̄ 4̆ 5̆ 6̄ 7̆ 8̆ 9̄ 10̆ 11̆ 12̄ 13̆ 14̆ 15̄ 16̄̆ {55|56}
If we allow for the replacement of 1̄̆ 2̄̆ by 1̄ 2̄ or 1̄ 2̆ 2̆½ and the optional replacement of – ⏑ ⏑ by – – anywhere from slots 3 through 14, then our pher3d schema is an adequate means of describing the epic hexameter. For the present, of course, it remains just that and nothing more.We may test the pher3d hypothesis by applying it to the problem of the major word-breaks in epic hexameter. In terms of our metrical schema, they are found in the following positions:
1̄̆ 2̄̆ 3̄ ͎4̆ 5̆ 6̄ ͎7̆ ͎8̆ 9̄ ͎10̆ 11̆ ͎12̄ 13̆ 14̆ 15̄ 16̄̆
… 3̄ ||, trithemimeral caesura
… 6̄ ||, penthemimeral caesura
… 7̄ ||, trochaic caesura
… 9̄ ||, hephthemimeral caesura
… 11̆ ||, bucolic diaeresis
Of course, some of these word-breaks are more important than others, and the occurrences of each vary from hexameter to hexameter in any given epic text. Only the penthemimeral and trochaic caesuras approach the status of invariables, with one or the other occurring in about 99% of Homeric hexameters. Beyond these two, the figures drop sharply. The next most common type of word-break, the bucolic diaeresis, occurs in about 60% of Homeric hexameters. [15] The dynamics of these various patterns have been the subject of much fruitful study leading to a {56|57} refined appreciation of epic meter and its relation to diction, [16] but there has been no successful application to “a problem like that of the aetiology of a complicated metrical form.” [17] Perhaps the word-breaks do tell us something about the origins of epic hexameter, but it is difficult to understand such regular variations as the one between the penthemimeral and trochaic caesuras. Are we to suppose that the hexameter was partially built from smaller metrical units shaped either ⏓ ⏓ – ⏑ ⏑ – or ⏓ ⏓ – ⏑ ⏑ – ⏑? Even if it were so, how would we explain the metrical sequences that follow these shapes in hexameter? Presumably, we would have to divide ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ and ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ into smaller units with shapes depending on whether the next word-break is a hephthemimeral caesura or a bucolic diaeresis. And what about those instances in hexameter where both occur? In aword, the problems are endless if we assume that the five major word-breaks of hexameter mark the junctures of smaller meters. As an alternative, I will apply Parry’s theory that these word-breaks mark the junctures of formulas.… 3̄ ||, trithemimeral caesura
… 6̄ ||, penthemimeral caesura
… 7̄ ||, trochaic caesura
… 9̄ ||, hephthemimeral caesura
… 11̆ ||, bucolic diaeresis
In his thèse complémentaire, [18] Parry has shown that two of the most common metrical irregularities in Homeric hexameter occur regularly at the five major word-breaks: {57|58}
(a) short in place of expected long before
trithemimeral caesura – ⏔ ⏑͎ || ⏔ – ⏔ – ⏔ – ⏔ – ⏓
penthemimeral caesura – ⏔ – ⏔ ⏑͎ || ⏔ – ⏔ – ⏔ – ⏓
hephthemimeral caesura – ⏔ – ⏔ – ⏔ ⏑͎ || ⏔ – ⏔ – ⏓
penthemimeral caesura – ⏔ – ⏔ ⏑͎ || ⏔ – ⏔ – ⏔ – ⏓
hephthemimeral caesura – ⏔ – ⏔ – ⏔ ⏑͎ || ⏔ – ⏔ – ⏓
(b) short vowel in hiatus before
trochaic caesura – ⏔ – ⏔ – ⏑͎ || ⏑ – ⏔ – ⏔ – ⏓
bucolic diaeresis – ⏔ – ⏔ – ⏔ – ⏑ ⏑͎ || – ⏔ – ⏓
These metrical irregularities, Parry noticed, result from formulaic juxtapositions. As a random selection of respective examples, consider the following sets of Homeric hexameters. In the first member of each set, there is a metrical irregularity caused by juxtaposition of a formula. In the second member, we see the same formula juxtaposed in a metrically regular context.
bucolic diaeresis – ⏔ – ⏔ – ⏔ – ⏑ ⏑͎ || – ⏔ – ⏓
(a) μεccηγὺ͎c || ʼΙθάκηc τε cάμοιό τε παιπαλοέccηc (δ 845)
vs. metrically regular
μεccηγὺc || Τεvέδοιο καὶ ʼ ́Ιμβρου παιπαλοέccηc (N 33)
vs. metrically regular
μεccηγὺc || Τεvέδοιο καὶ ʼ ́Ιμβρου παιπαλοέccηc (N 33)
θώρηκοc γύαλο͎ν||ἀπὸ δ’ ἔπτατο πικρὸc ὀιcτόc (N 587)
vs. metrically regular
θώρηκοc γύαλον||διὰδ’ ἔπτατο πικρὸc ὀιcτόc (E 99)
vs. metrically regular
θώρηκοc γύαλον||διὰδ’ ἔπτατο πικρὸc ὀιcτόc (E 99)
ἔνθεν δὲ προτέρω πλέομε͎ν||ἀκαχήμενοι ἦτορ (ι 62, etc.)
vs. metrically regular
ἑξῆμαρ μὲν ὁμῶc πλέομεν||νύκταc τε και ἦμαρ (κ 80, etc.) {58|59}
vs. metrically regular
ἑξῆμαρ μὲν ὁμῶc πλέομεν||νύκταc τε και ἦμαρ (κ 80, etc.) {58|59}
(b) λαῶν οἵ οἱ ἕποντο͎||ἀπ’ Αἰcήποιο ρʽοάων (Δ 91)
vs. metrically regular
λαῶν οἵ οἱ ἕποντο||Τρίκηc ἐξ ἱπποβότοιο (Δ 202)
vs. metrically regular
λαῶν οἵ οἱ ἕποντο||Τρίκηc ἐξ ἱπποβότοιο (Δ 202)
ἀλλ’ ὅ γε μερμήριζε κατὰ φρένα͎||ὡc ʼΑχιλῆα” (B 3)
vs. metrically regular
τρὶc μὲν μερμήριξε κατὰ φρένᾳκαὶ κατὰ θυμόν (Θ 169)
I must stress that the process of formulaic juxtaposition is a basic feature of Greek epic versification, [19] not some sort of deviation from normal techniques. More often than not, this process may be expected to maintain instead of disturb metrical regularity. Where lapses do occur, we are dealing simply with minor faults within the larger framework of a metrically workable system. Accordingly, the second members of the sets listed above should not be viewed as models upon which the first members were imperfectly patterned. Both members of each set are formulaically regular. Each first member is cognate with the second, not derived from it. Here we have the essence of an important yet elusive aspect of Parry’s theory, which I would rephrase as follows: formulaic regularity takes precedence over metrical regularity. [20] Occasionally, formulaic regularity is achieved at the expense {59|60} of metrical regularity, and the first member of each set above is simply meant to serve as illustration of this hierarchy. The point remains that the poet does not create metrical licenses: he merely inherits them by virtue of inheriting the formulas with which he composes. [21] When we observe the “striking contrast between the care lavished on the inner metrics of the formulae and the indulgence extended to metrical faults at their junctures with other words or formulae,” [22] we must keep in mind that this “indulgence” is an archaism, not an innovation.vs. metrically regular
τρὶc μὲν μερμήριξε κατὰ φρένᾳκαὶ κατὰ θυμόν (Θ 169)
Let me restate the metrical irregularities at issue: (a) short in place of expected long before trithemimeral, penthemimeral, or hephthemimeral caesura; (b) short vowel in hiatus before trochaic caesura or bucolic diaeresis. Notice that both these features, short for long and short in hiatus, would cease to be metrical irregularities if they occurred in verse-final position rather than verse-medial position before caesura or diaeresis. Furthermore, we actually know that {60|61} these metrical irregularities occur for the most part in formula-final position. Consequently, I propose that the formulas that end in such metrical irregularities had originated from verses shorter than pher3d. In other words, the pher3d pattern of the archetypal epic hexameter had accommodated the formulas of shorter verses, and it is these formulas that eventually led to the attested caesura- and diaeresis-system of the larger verse.
Pursuing my main hypothesis that the epic hexameter originated from pher3d, I will first assume that the most obvious type of shorter verse capable of transferring its formulas to pher3d is the simple pher itself, ⏓ ⏓ – ⏑ ⏑ – ⏓. Let us examine how formulas shaped pher might fit into pher3d:
 Such original placements, I will argue, would have led to the generalization of word-break patterns after slot 7 (trochaic caesura), after slot 9 (hephthemimeral caesura), and after slot 11 (bucolic diaeresis).
Such original placements, I will argue, would have led to the generalization of word-break patterns after slot 7 (trochaic caesura), after slot 9 (hephthemimeral caesura), and after slot 11 (bucolic diaeresis).

Complete pher formulas could fit either segments A or B, though those that have any long syllable in the Aeolic base would have had to be screened out of A. Also, B would tend to exclude those complete pher formulas that have ⏑ ⏑, ⏑ –, or – ⏑ at the Aeolic base—in decreasing order of {61|62} unsuitability. These restrictions on the Aeolic base would have encouraged the incursion of partial pher formulas with the pattern – ⏑ ⏑ –⏓, which I symbolize as A’ B’ vs. A B in the schema above. That is, pher formulas shaped ⏓ ⏓ || – ⏑ ⏑ – ⏓, with word-break after the Aeolic base, could fit A’ or B’ with the actual omission of the segment shaped ⏓ ⏓. Since internal expansion by dactyls had originally occurred between ⏓ ⏓ and – ⏑ ⏑ – ⏓, [23] the segmentation ⏓ ⏓ || – ⏑ ⏑ – ⏓ should be commonplace in terms of the simple pher itself. As for the epic hexameter, the presence of complete/partial pher formulas in segments A/A’ [24] seems borne out by statistical evidence. A word-break after slot 9 occurs in 45.4% of Iliadic verses and in 51.7% of Odyssean verses. [25] Furthermore, 19.8% and 25.4% of Iliadic and Odyssean verses respectively have word-break after both slots 9 and 11, so that approximately one-fourth of Homeric verses have at least a formula-segment A when there is no formula-segment A’. [26] For an illustration of interacting A’/A formulas, consider the following doublet:
A’ … λῦcε δὲ γυῖα# (Δ 469, etc.)
– ⏑ ⏑ – ⏓ = pher minus Aeolic base
vs.
A … ὑπέλυcε δὲ γυῖα# (Ο 581, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher {62|63}
Such formulas are functional variants in Homeric diction, as we may see from the formal mirroring of the above expressions in the mediopassive voice: [27]
– ⏑ ⏑ – ⏓ = pher minus Aeolic base
vs.
A … ὑπέλυcε δὲ γυῖα# (Ο 581, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher {62|63}
A’ … λύντο δὲ γυῖα# (Η 16, etc.)
– ⏑ ⏑ – ⏓ = pher minus Aeolic base
vs.
A … ὑπελύντο δὲ γυῖα# (Π 341)
⏑ ⏑ –⏑ ⏑ – ⏓ = pher
– ⏑ ⏑ – ⏓ = pher minus Aeolic base
vs.
A … ὑπελύντο δὲ γυῖα# (Π 341)
⏑ ⏑ –⏑ ⏑ – ⏓ = pher
Because of the rhythmical differences between 1̄̆ 2̄̆ and 10̆ 11̆, where our current hypothesis has 1̄̆ 2̄̆ evolving into 1̄ 2̄ or 1̄ 2̆ 2̆½, we should not expect to find formulas shared by segments A and B. On the other hand, formulas shaped – ⏑ ⏑ – ⏓ may fit both segments A’ and B’. The shape – ⏑ ⏑ – ⏓ is familiar from Lyric, where it is called the Adonic after the famous Sapphic refrain
Among these formulas shaped – ⏑ ⏑ – ⏑, the proportion of occurrences in segments A’ vs. B’ suggests that the primary locus of diffusion was in the verse-ending, A’. In some instances, we may even find grammatical proof of A’-provenience. For example, the archaic neuter dual adjective φαεινώ (⏑ – –) in the verse-final formula ὄccε φαεινώ# (N 3 etc.) is switched to an innovated neuter plural φαεινά (⏑ – ⏑) in the corresponding formula which appears before the trochaic caesura, ὄccε φαεινά || (N 435)—this despite the fact that the substantive ὄccε remains a neuter dual. [29]
ὦ τὸν Ἄδωνιν (168LP)
– ⏑ ⏑ – ⏓
Among Adonic formulas shared by segments A’ and B’ of epic hexameter, there is one important restriction: B’ accommodates formulas shaped – ⏑ ⏑ – ⏑ but screens out those shaped – ⏑ ⏑ – –. In other words, formulas shared by A’/B’ have an overt short at slot 7 (⏑) and a latent short at slot 16 (⏓). From Hainsworth’s tables, [28] I cite the following list of Homeric formulas which occur in both {63|64} segments A’ and B’. At the right of each formula is the number of Homeric occurrences in the A’ and B’ positions respectively:
– ⏑ ⏑ – ⏓
| αἷμα κελαινόν | 6:4 | ἱερὰ καλά | 3:4 |
| αἴcιμα πάντα | 2:1 | ἴφια μῆλα | 10:3 |
| ὀξὺν ἄκοντα | 1:3 | νῆα μέλαιναν | 14:4 |
| ἄνδρα ἔκαcτον | 9:1 | νηυcὶ θοῇcι | 4:5 |
| θεῖοc ἀοιδόc | 11:1 | νύκτα μέλαιναν | 5:1 |
| θεῖον ἀοιδόν | 11:1 | αἴθοπα οἶνον | 16:2 |
| γαῖα μέλαινα | 5:1 | αἰπὺc ὄλεθροc | 23:2 |
| πατρίδα γαῖαν | 62:1 | αἰπὺν ὄλεθρον | 23:2 |
| ὀξέϊ δουρί | 13:3 | λυγρὸc ὄλεθροc | 12:4 |
| ὀξέα δοῦρα | 13:3 | λυγρὸν ὄλεθρον | 12:4 |
| ἤματα πάντα | 26:4 | τεύχεα καλά | 10:7 |
| πᾶcι θεοῖcι | 12:2 | καμπύλα τόξα | 5:2 |
Adonic formulas may also occur at two other positions within the hexameter. One of these is {64|65} slots 1̄̆ 2̄̆ 3̄ 4̆; for example, νηυcὶ θοῇcι occurs in this position (δ 173) as well as in slots 12̄ 13̆ 14̆ 15̄ 16̆ (= A’) and 3̄ 4̆ 5̆ 6̄ 7̆ (= B’). We see here an innovation in terms of our hypothesis, since such a placement would be possible only after the Aeolic base 1̄̆ 2̄̆ was replaced by a dactylic 1̄ 2̆ 2̆½. The second other position possible for Adonic formulas is 9̄ 10̆ 11̆ 12̄ 13̆; consider the 15 attestations of πατρίδα γαῖαν in these slots, vs. the 62 instances of the same formula in slots 12̄ 13̆ 14̆ 15̄ 16̆ (= A’) and the solitary instance in 3̄ 4̆ 5̆ 6̄ 7̆ (= B’). But this second too is an innovation, as we will see below. [30]
Of course, I do not intend to suggest that all B’ formulas stem from A’ counterparts. There are, in fact, several Homeric formulas shaped – ⏑ ⏑ – ⏑ which regularly occur in section B’, never in A’. Again using Hainsworth’s tables, [31] I cite the following examples, with the number of Homeric occurrences at the right:
On the basis of such evidence, I am reluctant to rule out at least the possibility that some complete or partial pher formulas were originally restricted to the opening of the pher3d meter. {65|66} Of course, there are also a vast number of formulas shaped – ⏑ ⏑ – ⏑ that are restricted to the ending of the hexameter. Consider the following list of Homeric formulas that occur in A’ but never in B’: [32]
| ἄλγεα πολλά | 2 | θερμὰ λοετρά | 2 |
| ἄλκιμον ἔγχοc | 8 | ἴκμενον οὖρον | 3 |
| ἕβδομον ἦμαρ | 2 | πῦρ ἀίδηλον | 2 |
| λʽcτία λευκά | 2 | ἄξιον ὦνον | 2 |
| πατρὶc ἄρουρα | 3 | κῆρα μέλαιναν | 17 |
| φαίδιμα γυῖα | 7 | καλὰ πέδιλα | 12 |
| μείλινον ἔγχοc | 6 | νήπια τέκνα | 14 |
| ὄβριμον ἔγχοc | 13 | νώροπα χαλκόν | 5 |
Besides formulas shaped – ⏑ ⏑ – ⏓, there is also another readily available configuration of partial pher formulas, namely ⏑ ⏑ – ⏓ (from ⏓ ⏓ – || ⏑ ⏑ – ⏓). Parallel to the A’/B’ alternation of formulas shaped – ⏑ ⏑ – ⏑, we find an a/b alternation of formulas shaped ⏑ ⏑ – ⏑:
 What follows is a list of examples, [33] with the number of Homeric a vs. b occurrences at the right:
What follows is a list of examples, [33] with the number of Homeric a vs. b occurrences at the right:
Again, we also find formulas shaped ⏑ ⏑ – ⏑ which occur in section b to the exclusion of a, such {66|67} as [34]
or in section a to the exclusion of b, such as [35]

| βέλοc ὠκύ | 2:5 | φίλον ἦτορ | 32:4 |
| γάλα λευκόν | 1:1 | ξίφοc ὀξύ | 6:7 |
| δύο δοῦρε | 5:2 | μέλαν αἷμα | 3:3 |
| μέθυ ἡδύ | 6:3 | κλέοc ἐcθλόν | 2:5 |
| ἄορ ὀξύ | 3 | λιγὺc οὖροc | 2 |
| μέγα τεῖχοc | 5 | πατέρ’ ἐcθλόν | 6 |
| θοὸν ἅρμα | 2 | cτατὸc ἵπποc | 2 |
| πρόπαν ἦμαρ | 10 | κλέοc εὐρύ | 7 |
| μένοc ἠύ | 6 | μέγα ἄcτυ | 2 |
| ὄροc αἰπύ | 4 | μέγα λαῖτμα | 2 |
| ταχὺc υἱόc | 2 | βροτὸc ἄλλοc | 6 |
| κακὸν ἦμαρ | 7 | βροτὸν ἄλλον | 6 |
So far, I have tried to motivate the epic word-breaks after slot 7 (trochaic caesura), slot 9 (hephthemimeral caesura), and slot 11 (bucolic diaeresis) by assuming the accommodation of complete or partial pher formulas within a pher3d meter:
 There remains the task of motivating the functional variant of the trochaic caesura in epic hexameter, namely the penthemimeral caesura (word-break after slot 6). I propose that this pattern arose from the accommodation of formulas shaped pherd, specifically ⏑ ⏑ – ⏑ ⏑ –⏑ ⏑ – ⏓ = bracket C: {67|68}
There remains the task of motivating the functional variant of the trochaic caesura in epic hexameter, namely the penthemimeral caesura (word-break after slot 6). I propose that this pattern arose from the accommodation of formulas shaped pherd, specifically ⏑ ⏑ – ⏑ ⏑ –⏑ ⏑ – ⏓ = bracket C: {67|68}
 Consider the following sets of A vs. C formulas lodged in the endings of Homeric hexameters:
Consider the following sets of A vs. C formulas lodged in the endings of Homeric hexameters:


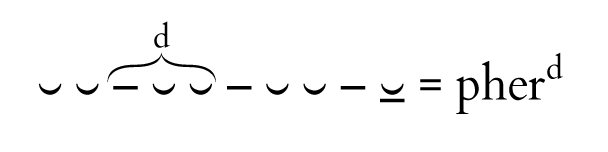
A … δέπαc ἀμφικύπελλον# (Α 584, etc.)
⏑ ⏑ – ⏑ – ⏑ – ⏓ = pher
vs.
C … δέπαc οἴcεται ἀμφικύπελλον (Ψ 663, etc.)
A … νέαc ἀμφιέλιccαc# (Ρ 612, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … νέεc ἤλυθον ἀμφιέλιccαι# (Ν 174, etc.)

A … βοὸc ἀγραύλοιο# (Κ 155, etc.)
⏑ ⏑ – ⏔ – ⏓ = pher
vs.
C … βοὸc ἔρχεται ἀγραύλοιο# (Χ 403)
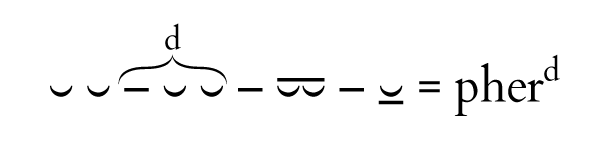
A … χθονὶ πουλυβοτείρῃ# (Γ 89, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … χθονὶ πίλνατο πουλυβοτείρῃ” (Ψ 368)
 {68|69}
{68|69}
A … χροὸc ἀνδρομέοιο# (Ρ 571, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … χροὸc ἄμεναι ἀνδρομέοιο# (Φ 70)

Such formulaic intrusions of οἴcεται, ἤλυθον, ἔρχεται, πίλνατο, ἄμεναι in Epic correspond to the metrical intrusions of the dactyl in Lyric, a process that I have called internal expansion. [36] ⏑ ⏑ – ⏑ – ⏑ – ⏓ = pher
vs.
C … δέπαc οἴcεται ἀμφικύπελλον (Ψ 663, etc.)
A … νέαc ἀμφιέλιccαc# (Ρ 612, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … νέεc ἤλυθον ἀμφιέλιccαι# (Ν 174, etc.)
A … βοὸc ἀγραύλοιο# (Κ 155, etc.)
⏑ ⏑ – ⏔ – ⏓ = pher
vs.
C … βοὸc ἔρχεται ἀγραύλοιο# (Χ 403)
A … χθονὶ πουλυβοτείρῃ# (Γ 89, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … χθονὶ πίλνατο πουλυβοτείρῃ” (Ψ 368)
A … χροὸc ἀνδρομέοιο# (Ρ 571, etc.)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … χροὸc ἄμεναι ἀνδρομέοιο# (Φ 70)
In this connection, I now cite another factor in lyric meter for which we find an analogue in epic formula: [37]
 Although d’ was the model of d from the standpoint of my reconstruction, it is bound to lose any formal distinction from the plain dactyl. From the mechanical standpoint of poetic composition, the d’ of an expanded pher is perceived simply as one of a series of dactyls, with the series framed by ⏓ ⏓ on one side and – ⏓ on the other. It follows from this inherent symmetry that the dynamics of prosody allow for dactylic expansion {69|70} of a formula at either of two junctures rather than at only one:
Although d’ was the model of d from the standpoint of my reconstruction, it is bound to lose any formal distinction from the plain dactyl. From the mechanical standpoint of poetic composition, the d’ of an expanded pher is perceived simply as one of a series of dactyls, with the series framed by ⏓ ⏓ on one side and – ⏓ on the other. It follows from this inherent symmetry that the dynamics of prosody allow for dactylic expansion {69|70} of a formula at either of two junctures rather than at only one:
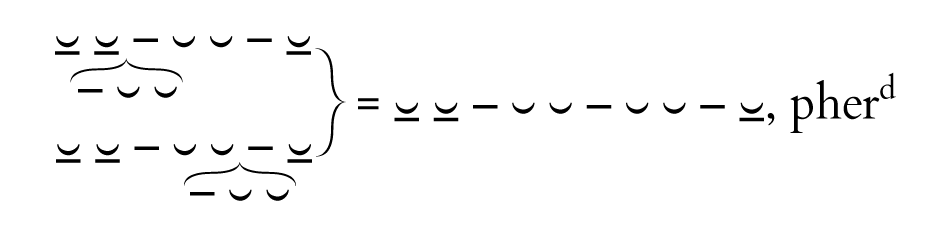 As we have just seen, alternations between formulas shaped pher and pherd in epic hexameter reveal expansions of the type
As we have just seen, alternations between formulas shaped pher and pherd in epic hexameter reveal expansions of the type
 In such instances, the formulaic expansions of Epic match the metrical expansion of Lyric. Accordingly, I should also expect epic hexameter to reveal formulaic expansion of the type
In such instances, the formulaic expansions of Epic match the metrical expansion of Lyric. Accordingly, I should also expect epic hexameter to reveal formulaic expansion of the type
 For verification, consider the following sets of A vs. C formulas in the endings of Homeric hexameter:
For verification, consider the following sets of A vs. C formulas in the endings of Homeric hexameter:

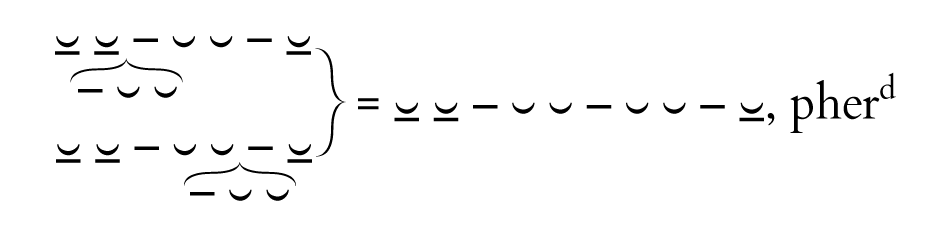
A … μεγαλήτορι θυμῷ#” (Ι 109)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … μεγαλήτορι ἥνδανε θυμῷ# (Ο 674)

A … περικαλλέα δίφρον# (υ 387)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … περικαλλέα βήcετο δίφρον# (Γ 262)
 {70|71}
{70|71}
A … κορυθαίολοc Ἕκτωρ# (passim)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … κορυθαίολοc ἠγάγεθ’ Ἕκτωρ# (Χ 471)

A … Τελαμώνιοc Αἴαc# (passim)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … Τελαμώνιοc ἄλκιμοc Αἴαc# (Μ 349)

A … φύγαδ’ ἔτραπεν ἵππουc# (Θ 257)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … φύγαδ’ ἔτραπε μώνυχαc ἵππουc# (Θ 157)

Again, the formulaic expansions with ἥνδανε, βήcετο, ἠγάγεθ’, ἄλκιμοc, μώνυχαc in Epic correspond to metrical expansions with the dactyl in Lyric.⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … μεγαλήτορι ἥνδανε θυμῷ# (Ο 674)
A … περικαλλέα δίφρον# (υ 387)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … περικαλλέα βήcετο δίφρον# (Γ 262)
A … κορυθαίολοc Ἕκτωρ# (passim)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … κορυθαίολοc ἠγάγεθ’ Ἕκτωρ# (Χ 471)
A … Τελαμώνιοc Αἴαc# (passim)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … Τελαμώνιοc ἄλκιμοc Αἴαc# (Μ 349)
A … φύγαδ’ ἔτραπεν ἵππουc# (Θ 257)
⏑ ⏑ – ⏑ ⏑ – ⏓ = pher
vs.
C … φύγαδ’ ἔτραπε μώνυχαc ἵππουc# (Θ 157)
At this point, a word of caution is in order. I am not claiming that dactylic expansion of formulas at the end of epic hexameters should be viewed as some sort of operative device at the time of Homeric composition. Rather, the formulaic variants shaped … ⏑ ⏑ || – ⏑ ⏑ – ⏓ vs. … ⏑ ⏑ || – ⏑ ⏑ || – ⏑ ⏑ – ⏓ and … ⏑ ⏑ – ⏑ ⏑ || – ⏓ vs. … ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ || – ⏓ are parallel inheritances. As such, I treat these formulaic patterns as survivals of archaic precedents that {71|72} at various points of their evolution may or may not have triggered other precedents in epic formula and meter. My task now is to evaluate some of these other precedents, with the purpose of linking them to the phenomenon of dactylic expansion.
In the patterns

 we find an important application to epic meter as well as formula. Let us begin with the obvious. The word-breaking pattern
we find an important application to epic meter as well as formula. Let us begin with the obvious. The word-breaking pattern
 besides
besides
… ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ || – ⏓
is a common phenomenon of epic hexameter. Among Homeric words with the shape – –, 41% occur in the 6th foot. [38] By contrast, the word-breaking pattern
… ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – || ⏓
is rare. In Books Α Β Γ Δ Ε Ζ Ω α β γ ω, it occurs in only 1% of the hexameters. [39] Notice too that the word-breaking pattern
… ⏑ ⏑ – ⏑ || ⏑ – ⏑ ⏑ – ⏓
is even more rare, occurring in only 0.1% of {72|73} Homeric hexameters. In this instance, the constraint against word-breaking is so noticeable that it goes by a name, Hermann’s Bridge. [40] Let us now contrast these rare patterns
… ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – || ⏓
… ⏑ ⏑ – ⏑ || ⏑ – ⏑ ⏑ – ⏓
with the common patterns
… ⏑ ⏑ – ⏑ || ⏑ – ⏑ ⏑ – ⏓
… ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ || – ⏓
… ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓
I submit that we see here a reflex inherited by hexameter from pher and pherd formulas. A pher formula can be expected to shun the patterns
… ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓
⏓ ⏓ – ⏑ ⏑ – || ⏓
⏓ || ⏓ – ⏑ ⏑ – ⏓
for the simple reason that dactylic expansion could then result in pherd formulas shaped⏓ || ⏓ – ⏑ ⏑ – ⏓
The unwieldy succession of two monosyllabic {73|74} words in the first two of these four types rules them out as viable patterns. So far, then, the decisive factor seems to be the structure of a pherd, not that of a pher.
As a corollary to Hermann’s Bridge, we see a reflex of dactylic expansion in the marked avoidance of spondees in the 4th foot, slots 9̄ 10̆ 11̆, if a word-break follows. This word-break is the bucolic diaeresis:
1̄̆ 2̄̆ 3̄ 4̆ 5̆ 6̄ 7̆ 8̆ 9̄ 10̆ 11̆||12̄ 13̆ 14̆ 15̄ 16̄̆
I have already discussed this constraint against spondaic word-endings in general terms of ictus. To be more specific now, I note that the innovation of substituting one long for two shorts has significantly pervaded the 4th foot. Spondees occur there with noticeable frequency. Here are statistics from a sample of 12,866 Homeric verses, the first twenty books of the Iliad:
in 1st foot, 5,070 spondees
in 2nd foot, 5,171 spondees
in 3rd foot, 1,966 spondees
in 4th foot, 3,849 spondees (!)
in 5th foot, 788 spondees [41]
Thus the proportion of dactyl to spondee in the 4th foot, 2.3 to 1, does not differ appreciably from the overall average for the first four feet of hexameter, which is, 2.6 dactyls to 1 spondee. [42] By contrast, when a word-break occurs after slot {74|75} 11, dactyls (9̄ 10̆ 11̆) outnumber spondees (9̄ 10 =̄ 11) 8 to 1; when there is a clause-break after 11, the figure is even higher, 20 to 1. [43] Where a word shaped … – ⏑ might have ended at 9 10, we find instead a variant shaped … – ⏑ ⏑ covering 9 10 11. I choose my examples from Meister’s collection: [44]
in 2nd foot, 5,171 spondees
in 3rd foot, 1,966 spondees
in 4th foot, 3,849 spondees (!)
in 5th foot, 788 spondees [41]
πτολιπόρθιον at 7 8 9 10 11 (ι 504, 530)
vs.
πτολίπορθοc, etc. elsewhere (passim)
vs.
πτολίπορθοc, etc. elsewhere (passim)
ἀέθλια at 8 9 10 11 (θ 108, φ 62)
vs.
ἄεθλον, ἄεθλα, etc. elsewhere (ca. 30x)
vs.
ἄεθλον, ἄεθλα, etc. elsewhere (ca. 30x)
Αἰτώλιοc at 7=8 9 10 11 (Δ 399)
vs.
Αίτωλόc elsewhere (Δ 527, etc.)
vs.
Αίτωλόc elsewhere (Δ 527, etc.)
δαφοινεόν at 8 9 10 11 (Σ 538)
vs.
δαφοινόc, etc. elsewhere (Β 308, etc.)
From such formulaic evidence, I infer that ictus, Hermann’s Bridge, bucolic diaeresis, and the dactyl preceding it are all interlocking phenomena, reflecting an original pherd formulaic structure with dactylic expansion between ⏑ ⏑ and – ⏑ ⏑ – ⏓. The expansion results in the word-breaking pattern … ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓ of epic hexameter.vs.
δαφοινόc, etc. elsewhere (Β 308, etc.)
It remains to ask why the expansion does not leave an equally distinct imprint on the other side of the dactylic shape. To put it another way, the question is why we should not find the pattern
…|| ⏑ ⏑ || – ⏑ ⏑ || – ⏑ ⏑ – ⏓
as consistently as the pattern
…|| ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓
I propose that the answer lies in the alternative pattern of dactylic expansion, between ⏑ ⏑ – ⏑ ⏑ and – ⏓. The pherd formulas with this shape should yield the following pattern within the meter of pher3d:
…|| ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ || – ⏓
The result is a strong precedent for formulas before the bucolic diaeresis which are shaped ⏑ ⏑ – ⏑ ⏑ without necessarily having word-break between ⏑ ⏑ and – ⏑ ⏑: hence the type πτολιπόρθιον.We are still left with the major problem of accounting for formulaic elements shaped ⏑ – ⏑ ⏑ before the bucolic diaeresis, such as ἀέθλια, δαφοινεόν, etc. Notice that the word-break preceding such shapes is the trochaic caesura: {76|77}
 I have already proposed that the trochaic caesura is a reflex of pher formulas placed at the opening of a pher3d meter, resulting in what I will now call segment X. This explanation of the trochaic caesura will have to be modified in the succeeding discussion, and we may start by asking the obvious question: what is segment y? I submit that this y is by nature a pherd formula minus the first syllable. From the metrical point of view, we could call it an acephalic pherd (= ^pherd). Of course, this hypothesis will have to be reconciled with the functional variant of the trochaic caesura, the penthemimeral caesura:
I have already proposed that the trochaic caesura is a reflex of pher formulas placed at the opening of a pher3d meter, resulting in what I will now call segment X. This explanation of the trochaic caesura will have to be modified in the succeeding discussion, and we may start by asking the obvious question: what is segment y? I submit that this y is by nature a pherd formula minus the first syllable. From the metrical point of view, we could call it an acephalic pherd (= ^pherd). Of course, this hypothesis will have to be reconciled with the functional variant of the trochaic caesura, the penthemimeral caesura:
 (To justify my designation of functional variant, let me reiterate: in 99% of the Homeric hexameters, we find either a trochaic caesura or a penthemimeral caesura.) Did Y/y originate from formulas shaped pherd/^pherd?
(To justify my designation of functional variant, let me reiterate: in 99% of the Homeric hexameters, we find either a trochaic caesura or a penthemimeral caesura.) Did Y/y originate from formulas shaped pherd/^pherd?


Before going any further, I must first refine my definition of sector Y. We expect it to contain formulas shaped pherd, but its formulas need not consistently bear the overt marks of dactylic expansion. We have already seen that the word-break patterns
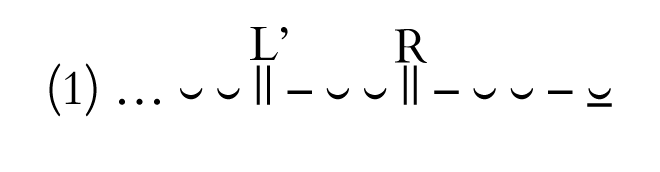 and
and
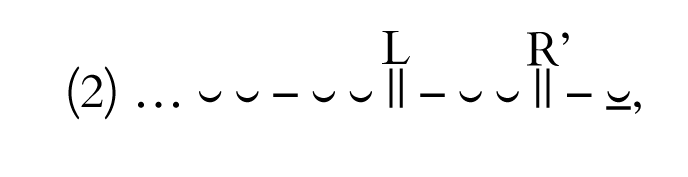 {77|78} which preserve both frames of internal dactylic expansion, are not nearly as frequent as the pattern containing only the bucolic diaeresis,
{77|78} which preserve both frames of internal dactylic expansion, are not nearly as frequent as the pattern containing only the bucolic diaeresis,
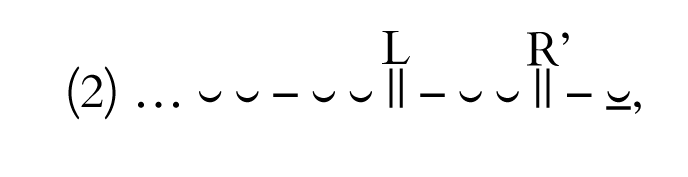
… ⏑ ⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓,
where only the right frame (R) of pattern 1 and the left frame (L) of pattern 2 survive. The statistical predominance of the bucolic diaeresis, which occurs in about 60% of Homeric hexameters, is due partially to the convergence of R and L. On the other hand, the divergence of R’ and L’, which mark the two divergent ways of expanding pher into pherd, weakens the precedent for observing word-break at either of those two places. In short, the word-break patterns in sector Y of epic hexameter, ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓, serve to show that it is by origin the locus of pherd formulas, but we must now shift from the standpoint of reconstruction to that of current dynamics in the Homeric composition of verses.In the verses of the Iliad and Odyssey, the formulaic input of sector Y is not confined to pherd formulas. Granted, I am arguing that pherd formulas had provided the initial precedent for the shape of sector Y, as I infer from the statistics of word-break and word-bridge patterns (especially the bucolic diaeresis and Hermann’s Bridge) and from the shapes of formulas like
 A partial pher formula like πατρίδα γαῖαν, which occurs 62 times in sector A of Homeric hexameter, also occurs 15 times in sector A’’. From Hainsworth’s tables, [47] I cite the following additional examples, with the respective number of Homeric A vs. A’’ occurrences at the right:
A partial pher formula like πατρίδα γαῖαν, which occurs 62 times in sector A of Homeric hexameter, also occurs 15 times in sector A’’. From Hainsworth’s tables, [47] I cite the following additional examples, with the respective number of Homeric A vs. A’’ occurrences at the right:
The subordination of these partial pher formulas to a larger pherd framework is also made evident {70|80} by an interesting constraint. If a formula shaped – ⏑ ⏑ – ⏑ is to be switched from sector A to sector A’’, it must not consist of a two-syllable word followed by a three-syllable word. Notice that such a combination would violate the pattern of dactylic expansion in a pherd. In terms of a pherd formula within a pher3d meter, dactylic hexameter requires a word-break after slot 11 rather than 10. To rephrase from the standpoint of epic hexameter as it is attested in the Homeric phase, we may say that such a combination would violate Hermann’s Bridge.
…||δέπαc||οἴcεται||ἀμφικύπελλον# (Ψ 663, etc.)
…||περικαλλέᾳβήcετο||δίφρον# (Γ 262)
Nevertheless, within the doubtless lengthy {78|79} prehistory of epic hexameter, sector Y must have evolved a formulaic framework that is more versatile than that of any original pherd formulas. Within the format of Epic, pherd formulas could not exist in their own right, but rather, must have coexisted with partial or complete pher formulas encased at the end of a pher3d meter. There is, however, an observable hierarchy between such pherd and pher formulas, in that the second are subordinate to the first. For example, partial pher formulas shaped – ⏑ ⏑ – ⏑ may shift positions within the framework of a pherd or ^pherd pattern (slots 7-16 or 8-16):…||περικαλλέᾳβήcετο||δίφρον# (Γ 262)

| δώματα καλά | 8:3 | οὐρανὸν εὐρύν | 7:25 |
| ἀγλαὰ δῶρα | 13:7 | αἴθοπα οἶνον | 16:2 |
| νόcτιμον ἦμαρ | 7:4 | ἄλκιμον ἦτορ | 2:2 |
| ὅρκια πιcτά | 4:7 | δένδρεα μακρά | 1:3 |
Besides partial pher formulas shaped – ⏑ ⏑ – ⏑, those shaped ⏑ ⏑ – ⏑ are also found in shifting positions within the framework of a pherd or ^pherd pattern (slots 7-16 or 8-16):
 From Hainsworth’s tables, [48] I cite the following examples, with the respective number of Homeric a vs. a’’ occurrences at the right:
From Hainsworth’s tables, [48] I cite the following examples, with the respective number of Homeric a vs. a’’ occurrences at the right:
Here too we find a constraint that illustrates the subordination of these partial pher formulas {80|81} to a larger pherd framework. Formulas shaped ⏑ ⏑ || – ⏑ may be shifted from slots 13 14 15 16 (= a) into slots 10 11 12 13 (= a’’), but not into slots 7 8 9 10. Such a shift would violate the pattern of dactylic expansion in a pherd. In terms of a pherd formula within a pher3d meter, dactylic expansion requires a word-break after slot 11 rather than 10. Again, I have expressed this constraint from the standpoint of my reconstruction. From the standpoint of the hexameter as it is attested in the Homeric phase, we may again say instead that such a shift would violate Hermann’s Bridge.

| ξίφοc ὀξύ | 6:4 | φίλον ἦτορ | 32:4 |
| χρόα καλόν | 3:5 | μέγα λαῖτμα | 2:3 |
| φρεcὶ cῇcι | 3:17 | μέλαν αἷμα | 3:1 |
| φρεcὶ ᾗcι | 3:17 | κλέοc ἐcθλόν | 2:4 |
To sum up: sector Y(/y) of epic hexameter is a composite that evolved out of pherd (/^pherd) and pher formulaic elements. We see the traces of these elements in the following word-break patterns:
 {81|82} It is, then, an oversimplification to say that sector Y consists of pherd formulas. Rather, it consists of formulas that evolved within the framework of a pherd formulaic structure.
{81|82} It is, then, an oversimplification to say that sector Y consists of pherd formulas. Rather, it consists of formulas that evolved within the framework of a pherd formulaic structure.

Having recorded this important qualification, I return to the problem of the two fundamental caesuras in epic hexameter, the penthemimeral and the trochaic:

 Notice that Homeric formulas shaped Y have functional variants shaped y: [49]
Notice that Homeric formulas shaped Y have functional variants shaped y: [49]


Y … θάνατον καὶ κῆρα μέλαιναν# (β 283, etc.)
y … φόνον καὶ κῆρα μέλαιναν# (Ε 652 = Λ 443)
Y … κραδίη καὶ θυμὸc ἀγήνωρ# (Κ 220, etc.)
y … μένοc καὶ θυμὸc ἀγήνωρ# (Υ 174)
Y … πολέων δ’ ἀπὸ θυμὸν ἕλοιτο# (E 691)
y … πολέων δ’ ἀπὸ θυμὸν ἕλοιτο # (Π 655) {82|83}
Y … ἐμίγη φιλότητι καὶ εὐνῇ# (ψ 219)
y … μίγη φιλότητι καὶ εὐνῇ# (Ζ 25)
Y … προcεφώνεε φαίδιμοc υἱόc# (Φ 152, etc.)
y … προcηύδα φαίδιμοc υἱόc# (Ζ 144, Φ 97).
y … φόνον καὶ κῆρα μέλαιναν# (Ε 652 = Λ 443)
Y … κραδίη καὶ θυμὸc ἀγήνωρ# (Κ 220, etc.)
y … μένοc καὶ θυμὸc ἀγήνωρ# (Υ 174)
Y … πολέων δ’ ἀπὸ θυμὸν ἕλοιτο# (E 691)
y … πολέων δ’ ἀπὸ θυμὸν ἕλοιτο # (Π 655) {82|83}
Y … ἐμίγη φιλότητι καὶ εὐνῇ# (ψ 219)
y … μίγη φιλότητι καὶ εὐνῇ# (Ζ 25)
Y … προcεφώνεε φαίδιμοc υἱόc# (Φ 152, etc.)
y … προcηύδα φαίδιμοc υἱόc# (Ζ 144, Φ 97).
The Y/y variations are especially noticeable when they are composed entirely of epithet + name combinations, as in the genitive singular:
Y … ἑκατηβόλου ʼΑπόλλωνοc# (Α 370, etc.)
y … ἑκηβόλοὐ Απόλλωνοc# (Α 14, 373)
Turning to corresponding epithet + name combinations in the nominative singular, however, we find a highly interesting constraint in Homeric diction. Despite numerous instances of epithet + name shaped y, there is a marked absence of variants shaped Y applying to the same person. For example, consider the lack of Y formulas corresponding to the following designations with y formulas:
y … ἑκηβόλοὐ Απόλλωνοc# (Α 14, 373)
… πολύτλαc δῖοc ʼΟδυccεύc# 38 times
… ἄναξ ἀνδρῶν ʼΑγαμέμνων# 37 times
… Γερήνιοc ἱππότα Νέcτωρ# 31 times
… βοὴν ἀγαθὸc Μενέλαοc# 20 times
… μέγαc κορυθαίολοc Ἕκτωρ# 12 times
As Parry has noticed, [50] there is a basic difference {83|84} in combinatory behavior between such nominative formulas and any corresponding genitive formulas. The first are normally subjects of preceding verbs, while the second serve as dependents of preceding nouns far more often than as objects of preceding verbs. [51] Parry infers that it may well be the shape of preceding verbs that results in the preponderance of nominatives shaped y over nominatives shaped Y. Let us examine the verbs immediately preceding a formula like πολύτλαc δῖοc ʼΟδυccεύc: μερμήριξε, ἦcθε (2x), ἄκουcε, ἐcάκουcε, καθεῦδε (2x), ἠρᾶτο, γήθηcε (2x), ἐνόηcε, ἀνάειρε (2x), θηεῖτο, ἄρχε (2x), ἐβόηcε, προcέειπε (8x). Parry links such formal evidence with a basic functional feature of Greek Epic. Consisting primarily of narrative, Homeric diction furthers the preponderance of past tense and third person, for which the basic Greek form is -ε. [52] If, the reasoning goes, the verb is to be placed immediately before the nominative epithet + noun combination, then our formula must be shaped ⏑ – ⏔ – ⏔ – ⏓ (= y) to make room for the last syllable of the verb. Presumably, any variant shaped ⏑ ⏑ – ⏔ – ⏔ – ⏓ (= Y) would not be of much use.… ἄναξ ἀνδρῶν ʼΑγαμέμνων# 37 times
… Γερήνιοc ἱππότα Νέcτωρ# 31 times
… βοὴν ἀγαθὸc Μενέλαοc# 20 times
… μέγαc κορυθαίολοc Ἕκτωρ# 12 times
It is possible to go beyond Parry’s analysis of the situation by reexamining it from the standpoint of X and x, the initial sectors of hexameter. The shape ⏓ ⏓ – ⏑ ⏑ – (= x) differs from the shape ⏓ ⏓ – ⏑ ⏑ – ⏑ (= X) in that it should not be {84|85} expected to end with a verb. So much for a reformulation; the problem is, it simply does not work. I can think of several Homeric verbs that could theoretically be placed in exactly this position, at the end of a sequence ⏓ ⏓ – ⏑ ⏑ –: ἀπέβη, μίγήἐμίγη, μετέφη, προcέφη, etc., not to mention any 3rd singular -εν followed by a consonant starting the next word. And yet, strangely, there is no such regular pattern in Homeric diction. For example, let us consider the common Homeric formula for introducing a speech:
X #τοῖcι δὲ καὶ μετέειπε||…
followed by such nominative epithet + name combinations as
…||Γερήνιοc ἱππότα Νέcτωρ#
…||βοὴν ἀγαθὸc Μενέλαοc#
…||ποδάρκηc δῖοc ʼΑχιλλεύc#
…||γέρων ἥρωc ʽΑλιθέρcηc#
…||θεὰ γλαυκῶπιc ʼΑθήνη#
etc.
Contrast the total absence of Homeric formulas shaped
…||βοὴν ἀγαθὸc Μενέλαοc#
…||ποδάρκηc δῖοc ʼΑχιλλεύc#
…||γέρων ἥρωc ʽΑλιθέρcηc#
…||θεὰ γλαυκῶπιc ʼΑθήνη#
etc.
*x #τοῖcι δὲ καὶ μετέφη||…
In fact, Homeric diction never features μετέφη before the penthemimeral caesura:
*x #– ⏑ ⏑ – μετέφη||…
And yet, there is no purely metrical factor that should prevent the occurrence of this verb μετέφη in the sequence ⏑ ⏑ – before the penthemimeral {85|86} caesura. Consider its regular placement in the sequence ⏑ ⏑ – before the hephthemimeral caesura:
τοῖcιν δ’ ʼΑντίνοοc μετέφῃ || Εὐπείθεοc υἱόc (δ 660, etc.)
τοῖc δὲ δολοφρονέων μετέφῃ || πολύμητιc ʼΟδυccεύc (σ 51, φ 274)
etc.
Even on those rare occasions when a nominative epithet + name combination shaped Y is available, such as
τοῖc δὲ δολοφρονέων μετέφῃ || πολύμητιc ʼΟδυccεύc (σ 51, φ 274)
etc.
…||ἱερη ʼὶc Τηλεμάχοιο#
⏑ ⏑ – ⏔ – ⏑ ⏑ – ⏓,
the preceding formula (introducing a speech) eschews μετέφη:
⏑ ⏑ – ⏔ – ⏑ ⏑ – ⏓,
τοῖcι δὲ καὶ μετέειφ’||ἱερὴ ʼὶc Τηλεμάχοιο (β 409, etc.),
instead of
*τοῖcι δὲ καὶ μετέφη||ἱερὴ ʼὶc Τηλεμάχοιο.
Nor does it matter that μετέφη is here followed by a vowel. Consider again
τοῖcιν δ’ ʼΑντίνοοc μετέφη || Εὐπείθεοc υἱόc (δ 660, etc.) [53]
Why, then, does sector x fail to end with μετέφη? Since meter does not seem to be a direct factor, perhaps we should look to formulaic behavior for an answer. {86|87}Let us pursue the issue by taking up another example. We have a host of Homeric attestations for the formula
X # τὸν δ’ αὖτε προcέειπε||…,
but there is not a single instance of
*x # τὸν δ’ αὖτε προcέφη||…
In fact, out of the 213 instances of προcέφη in the Iliad and Odyssey, the word occurs 211 times before the hephthemimeral caesura, but only twice before the penthemimeral:
ὥc πού cε προcέφη||cοὶ δὲ φρέναc ἄφρονι πεῖθε (Π 842)
ἔνθα χ’ ὅμωc προcέφη||κεχολωμένοc, ἤ κεν ἐγὼ τόν” (λ 565)
The anomaly of these verses is noticeable not only from the position but also from the usage of προcέφη. Unlike the vast majority of Homeric verses containing προcέφη, these two neither introduce a quotation nor give the nominative epithet + noun for the person who is being quoted. Contrast the following familiar patterns:
ἔνθα χ’ ὅμωc προcέφη||κεχολωμένοc, ἤ κεν ἐγὼ τόν” (λ 565)
#τὸν δὲ ὑπόδρα ἰδὼν προcέφη||…
#καί μιν φωνήcαc προcέφη||…
#τὸν δ’ ἀπαμειβόμενοc προcέφη||…
…||κορυθαίολοc Ἕκτωρ#
…||πολύμητιc ʼΟδυccεύc#
…||πόδαc ὠκὺc ʼΑχιλλεύc#
etc.
The verb προcέφη can be followed by a subject {87|88} like
#καί μιν φωνήcαc προcέφη||…
#τὸν δ’ ἀπαμειβόμενοc προcέφη||…
…||κορυθαίολοc Ἕκτωρ#
…||πολύμητιc ʼΟδυccεύc#
…||πόδαc ὠκὺc ʼΑχιλλεύc#
etc.
…||μένοc ʼΑλκινόοιο # (η 178, etc.)
but not by
…||ἱερὸν μένοcʼΑλκινόοιο#.
The latter formula, shaped Y, is available as the subject, and yet we never find a Homeric verse shaped
*τὸν δ’ αὖτε προcέφη||ἱερὸν μένοc ʼΑλκινόοιο
The first part of such a verse, shaped x, is wanting. Furthermore, whenever it happens in the Odyssey that ἱερὸν μένοc ʼΑλκινόοιο serves as subject of the clause, any verb immediately preceding it will originate not from some x formula, but from a modified X formula:
?||Y
αὐτὰρ ἐπεὶ τό γ’ ἄκουc’||ἱερὸν μένοc ʼΑλκινόοιο” (η 167)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||πολύτλαc δῖοc ʼΟδυccεύc (θ 446)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||Ποcειδάων ἐνοcίχθων (ν 159)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||βοὴν ἀγαθὸc Μενέλαοc (ο 92)
?||Y
τοῖcιν δ’ ἡγεμόνευ’||ἱερὸν μένοc ʼΑλκινόοιο (θ 4, 421)
X||y
τοῖcιν δ’ ἡγεμόνευε||Γερήνιοc ἱππότα Νέcτωρ (γ 386) {88|89}
?||Y
καὶ τὰ μὲν εὖ κατέθηχ’||ἱερὸν μένοc ʼΑλκινόοιο (ν 20)
X||y
καὶ τὰ μὲν εὖ κατέθηκε || λίθον δ’ ἐπέθηκε θύρῃcιν (ν 370)
?||Y
τοῖcι δὲ βοῦν ἱέρευc’||ἱερὸν μένοcʼΑλκινόοιο (ν 24)
X||y
τοῖcι δὲ βοῦν ἱέρευcε||ἄναξ ἀνδρῶν ʼΑγαμέμνων” (Η 314).
In such instances of ?||Y, I infer that there is no inherited formula x which would be available to take the place of X when a subject shaped Y takes the place of y. Furthermore, from our data on the verbs μετέφη and προcέφη, I infer that inherited x formulas resist verbs in final position. Note again the contrast with the X formulas, which regularly accommodate verbs in final position.αὐτὰρ ἐπεὶ τό γ’ ἄκουc’||ἱερὸν μένοc ʼΑλκινόοιο” (η 167)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||πολύτλαc δῖοc ʼΟδυccεύc (θ 446)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||Ποcειδάων ἐνοcίχθων (ν 159)
X||y
αὐτὰρ ἐπεὶ τό γ’ ἄκουcε||βοὴν ἀγαθὸc Μενέλαοc (ο 92)
?||Y
τοῖcιν δ’ ἡγεμόνευ’||ἱερὸν μένοc ʼΑλκινόοιο (θ 4, 421)
X||y
τοῖcιν δ’ ἡγεμόνευε||Γερήνιοc ἱππότα Νέcτωρ (γ 386) {88|89}
?||Y
καὶ τὰ μὲν εὖ κατέθηχ’||ἱερὸν μένοc ʼΑλκινόοιο (ν 20)
X||y
καὶ τὰ μὲν εὖ κατέθηκε || λίθον δ’ ἐπέθηκε θύρῃcιν (ν 370)
?||Y
τοῖcι δὲ βοῦν ἱέρευc’||ἱερὸν μένοcʼΑλκινόοιο (ν 24)
X||y
τοῖcι δὲ βοῦν ἱέρευcε||ἄναξ ἀνδρῶν ʼΑγαμέμνων” (Η 314).
For another striking example of X/x contrast, I cite the formulaic behavior of verbs in 3rd singular -ε plus movable ν before single consonant (C-) starting the next word. In Homeric diction, the pattern -εν||C- is extremely rare at the penthemimeral caesura, while it is relatively common at the hephthemimeral. Consider the following statistics: [54] {89|90}
I do not mean to suggest, however, that these verbs cannot end on syllable 6 of our schema for the hexameter:
| before penthemimeral | before hephthemimeral | |
| φέρεν ́ἔφερεν | 0 times | 9 times |
| ἵμαcεν | 0 times | 5 times |
| θῆκεν | 0 times | 7 times |
| δῶκεν | 0 times | 4 times |
| πόρεν | 0 times | 2 times |
| ἄγεν | 0 times | 2 times |
1̄̆ 2̄̆ 3̄ 4̆ 5̆ 6̄ ͎7̆ 8̆ 9̄ 10̆ 11̆ 12̄ 13̆ 14̆ 15̄ 16̄̆
Such verbs as δῶκεν can and do regularly end on syllable 6, but only if they are followed by a monosyllabic particle:
αὐτὰρ ἐπεὶ δῶκέν τε||καὶ ἔκπιον, αὐτίκ’ ἔπειτα (κ 237)
Technically, the initial part of this verse ends at the trochaic caesura, not the penthemimeral. The τε is syntactically dependent on and inseparable from the δῶκεν, so that the formula ends as … δῶκέν τε. In other words, δῶκεν functions here as part of an X rather than an x formula. What, then, would happen with such a combination at the hephthemimeral caesura? Let us compare the behavior of a verb like λοῦcεν when it ends at slot 6 as opposed to when it ends at slot 9:
… λοῦcέν τε||καὶ ἔχριcεν λίπ’ ἐλαίῳ# (γ 466, κ 364, 450)
… λοῦcεν||καὶ χρῖcεν ἐλαίῳ# (ψ 154, ω 366) {90|91}
The combination λοῦcέν τε καί would have been metrically impossible in the latter instance. If a verb ending at slot 9 is followed by a monosyllabic enclitic, this enclitic in turn must be followed by another enclitic:
… λοῦcεν||καὶ χρῖcεν ἐλαίῳ# (ψ 154, ω 366) {90|91}
… πόρεν δέ ἑ||Φαίδιμοc ἥρωc# (δ 617, ο 117)
… πόρεν δέ οἱ||ἀγλαὸν υἱόν# (Π 185)
… πόρεν δ’ ὅ γε||cήματα λυγρά# (Ζ 168)
… δῶκεν δέ μοι||εὖχοc ʼΑθήνη# (Η 154) [55]
In other words, Hermann’s Bridge is not violated. The central issue, however, remains this: when it ends at slot 6, a verb like λοῦcεν functions as part of an X rather than x formula.… πόρεν δέ οἱ||ἀγλαὸν υἱόν# (Π 185)
… πόρεν δ’ ὅ γε||cήματα λυγρά# (Ζ 168)
… δῶκεν δέ μοι||εὖχοc ʼΑθήνη# (Η 154) [55]
Consider also the common X formula
#ὣc φάτο μείδηcεν δὲ||…followed by such epithet + name combinations as
…||πολύτλαc δῖοc ʼΟδυccεύc#
…||βοὴν ἀγαθὸc Μενέλαοc#
…||θεὰ γλαυκῶπιcʼΑθήνη#
etc.
Other such formulas are {91||92}
…||βοὴν ἀγαθὸc Μενέλαοc#
…||θεὰ γλαυκῶπιcʼΑθήνη#
etc.
#ὣc φάτο γήθηcεν δὲ||…
#ὣc φάτο κώκυcεν δὲ||…
#ὣc φάτο ρʽίγηcεν δὲ||…
In these contexts, we even see two instances where the nominative epithet + name combination is shaped Y rather than y:
#ὣc φάτο κώκυcεν δὲ||…
#ὣc φάτο ρʽίγηcεν δὲ||…
ὣc φάτο μείδηcεν δ’||ἱερὴ ἲc Τηλεμάχοιο (π 476)
ὣc φάτο γήθηcεν δ’||ἱερὸν μένοc ʼΑλκινόοιο” (θ 385)
To accommodate Y, the original X is simply modified, apparently for lack of any inherited formulaic variant of X shaped x. Likewise, among the rare Homeric attestations of -εν||C- at the penthemimeral caesura, the x formula involved may be the result of modification instead of direct inheritance. For example, a line like
ὣc φάτο γήθηcεν δ’||ἱερὸν μένοc ʼΑλκινόοιο” (θ 385)
ὣc ἄρ’ ἐφώνηcεν||τῇ δ’ ἄπτεροc ἔπλετο μῦθοc (ρ 57, etc.)
seems to be part of a subset which includes the common types
ὣc ἄρα φωνήcαc||” (passim)
καί μιν φωνήcαc||ἔπεα πτερόεντα προcηύδα (passim)
Accordingly, the pattern ἐφώνηcεν||C- at the penthemimeral caesura cannot serve as counter-example to my argument that verbs in -εν are wanting at the end of inherited x formulas.καί μιν φωνήcαc||ἔπεα πτερόεντα προcηύδα (passim)
Let us return to the original problem as {92|93} viewed from Parry’s standpoint. He observed that there are very few occurrences of nominative epithet + noun formulas shaped
 What I am now proposing is that X is a repository of partial pher formulas shaped B’ and b, [57] and that it is this capacity that makes such a segment X distinct in formulaic behavior from x. This distinction, I should repeatedly emphasize, implies that X and x were not formulaic variants by origin.
What I am now proposing is that X is a repository of partial pher formulas shaped B’ and b, [57] and that it is this capacity that makes such a segment X distinct in formulaic behavior from x. This distinction, I should repeatedly emphasize, implies that X and x were not formulaic variants by origin.
⏑ ⏑ – ⏔ – ⏔ – ⏓,
as opposed to a multitude of functional equivalents shaped
⏑ – ⏔ – ⏔ – ⏓
What I am proposing here is that this Y/y distinction in formulaic behavior is but a symptom of a more basic x/X distinction. To rephrase the problem, we must ask why X may regularly end with a past 3rd singular verb, but not x. Parry’s solution for the Y/y distinction was that the past 3rd singular verbs that immediately precede the main caesura have the shape that requires a trochaic rather than penthemimeral caesura. It becomes obvious from our survey, however, that there are several past 3rd singular verbs that could ideally fit before the penthemimeral caesura and yet shun this very position. I infer that we see here an aspect of the formulaic heritage: formulas shaped x behave differently from those shaped X because they are not inherited variants. Consider such X formulas as
τοῖcι δὲ καὶ μετέειπε||…
τὸν δ’ αὖτε προcέειπε||…
ὣc φάτο γήθηcεν δὲ||…
ὣc φάτο ρʽίγηcεν δὲ||…
The verbs of these formulas recur in verse-final position as well: {93|94}
τὸν δ’ αὖτε προcέειπε||…
ὣc φάτο γήθηcεν δὲ||…
ὣc φάτο ρʽίγηcεν δὲ||…
… καὶ μετέειπεν# (Α 73, etc.)
… καί μιν προcέειπεν# (Α 441, etc.)
… γήθηcέν τε# (Π 530)
… ρʽίγηcέν τε#” (Π 119)
As I have already argued, [56] such interchange in positions before caesura and before verse-end is a characteristic of partial pher formulas:
… καί μιν προcέειπεν# (Α 441, etc.)
… γήθηcέν τε# (Π 530)
… ρʽίγηcέν τε#” (Π 119)

Going even further, we can say that ⏓ ⏓ – ⏑ ⏑ – ⏑ (= X) and ⏓ ⏓ – ⏑ ⏑ – (= x) cannot be interpreted as metrical variants either, since there is to my knowledge no such thing as an Aeolic meter shaped
*⏓ ⏓ – ⏑ ⏑ ⏓ = pher^ (catalectic pher)
derived from {94|95}
⏓ ⏓ – ⏑ ⏑ – ⏓ = pher
By contrast, y and Y are functional variants both from the standpoint of epic formula, as in
…||μίγη φιλότητι καὶ εὐνῇ# (Ζ 25)
…||ἐμίγη φιλότητι καὶ εὐνῇ# (ψ 219)
and from the standpoint of lyric meter:
…||ἐμίγη φιλότητι καὶ εὐνῇ# (ψ 219)
⏓ – ⏑ ⏑ – ⏑ ⏑ – ⏓ = ^pherd (acephalic pherd)
derived from
⏓ ⏓ – ⏑ ⏑ – ⏑ ⏑ – ⏓ = pherd
The two types ^pherd and pherd are metrical variants not only in structure but also in usage. Consider the lines of Sappho 111LP: [58]
ἴψοι δὴ τὸ μέλαθρον· – – – ⏑ ⏑ – ⏓ = pher
ὐμήναον·
ἀέρρετε τέκτονεc ἄνδρεc· ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ = ^pherd
ὐμήναον.
γάμβροc ἔρχεται ἴcοc Ἄρευι· – – – ⏑ ⏑ – ⏑ ⏑ – ⏓ = pherd
ἄνδροc μεγάλω πόλυ μέζων. – – ⏑ ⏑ – ⏑ ⏑ – ⏓ = ^pherd
Compare also the Rhodian folk-song known as the Chelidonismos or ‘Swallow Song’ (848P), where ^pher and pher are clearly variants in the first nine lines: {95|96}
ὐμήναον·
ἀέρρετε τέκτονεc ἄνδρεc· ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ = ^pherd
ὐμήναον.
γάμβροc ἔρχεται ἴcοc Ἄρευι· – – – ⏑ ⏑ – ⏑ ⏑ – ⏓ = pherd
ἄνδροc μεγάλω πόλυ μέζων. – – ⏑ ⏑ – ⏑ ⏑ – ⏓ = ^pherd
ἦλθ' ἦλθε χελιδὼν – – ⏑ ⏑ – ⏓ ^pher
καλὰc ὥραc ἄγουcα, – ⏑ – ⏑ ⏑ – ⏓ pher
καλοὺc ἐνιαυτούc, – – ⏑ ⏑ – ⏓ [59] ^pher
ἐπὶ γαcτέρα λευκά, ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
ἐπὶ νῶτα μέλαινα. ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
παλάθαν cὺ προκύκλει ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
ἐκ πίονοc οἴκου – – ⏑ ⏑ – ⏓ ^pher
οἴνου τε δέπαcτρον – – ⏑ ⏑ – ⏓ ^pher
τυροῦ τε κάνυcτρον. – – ⏑ ⏑ – ⏓ ^pher
The type pherd is used line-by-line (= κατὰ cτίχον) in Sappho 110LP, as also ^pherd + – ⏑ – ⏑ – ⏓ in Archilochos (168-171W). [60] In sum, the lyric metrical variation of verses shaped pherd and ^pherd corresponds to the epic formulaic {96|97} variation of segments shaped Y and y.καλὰc ὥραc ἄγουcα, – ⏑ – ⏑ ⏑ – ⏓ pher
καλοὺc ἐνιαυτούc, – – ⏑ ⏑ – ⏓ [59] ^pher
ἐπὶ γαcτέρα λευκά, ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
ἐπὶ νῶτα μέλαινα. ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
παλάθαν cὺ προκύκλει ⏑ ⏑ – ⏑ ⏑ – ⏓ pher
ἐκ πίονοc οἴκου – – ⏑ ⏑ – ⏓ ^pher
οἴνου τε δέπαcτρον – – ⏑ ⏑ – ⏓ ^pher
τυροῦ τε κάνυcτρον. – – ⏑ ⏑ – ⏓ ^pher
Once the innovation of substituting one long for two shorts takes effect in the evolution of the epic hexameter, any original ^pherd formulas shaped
– – ⏑ ⏑ – ⏑ ⏑ – ⏓ (which we will designate Y’)
may then be inserted in place of pherd formulas shaped
⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ (= Y)
From the metrical standpoint, the shape Y’ is a variant of Y. From the formulaic standpoint, however, Y’ may also be a variant of y:
y … ʼΟδυccῆοc θείοιο# (27 times)
Y’ … Λαερτιάδεω ʼΟδυcῆοc# (12 times)
y … Διὸc νεφεληγερέταο# (6 times)
Y’ … πατρὸc Διὸc αἰγιόχοιο# (3 times)
y … τά οἱ πόρε χάλκεοc Ἄρηc# (Η 146)
y … τά οἱ πόρε δῖα Καλυφώ# (ε 321, 372)
y … ἅ οἱ πόρε παρθένοc ἀδμήc# (ζ 228)
y … ὅ τοι πόρε ΦοῖβοcʼΑπόλλων# (Ο 441)
Y’ … τόν τοι πόρε πότνια μήτηρ# (Ψ 92)
Y’ … τήν οἱ πόρε ΦοῖβοcʼΑπόλλων# (Α 72, Λ 353)
Y’ … τήν οἱ πόρε δῖοc ʼΑχιλλεύc# (Ι 667) {97|98}
y … διῖ ́φιλοc||– ⏑ ⏑ – ⏓# (Κ 49, etc.)
Y’ … δουρίκλυτοc||– ⏑ ⏑ – ⏓# (Ν 210, etc.)
As Parry has noticed, [61] the epithets in the last example are found in complementary distribution. Either epithet can apply to any hero, depending on the space available before the bucolic diaeresis. After a trochaic caesura, use διΐφιλοc; after a penthemimeral, δουρίκλυτοc. We may wish to reinterpret as follows: διΐφιλοc and δουρίκλυτοc are reflexes of epithets that were originally meant to start ^pherd formulas shaped
Y’ … Λαερτιάδεω ʼΟδυcῆοc# (12 times)
y … Διὸc νεφεληγερέταο# (6 times)
Y’ … πατρὸc Διὸc αἰγιόχοιο# (3 times)
y … τά οἱ πόρε χάλκεοc Ἄρηc# (Η 146)
y … τά οἱ πόρε δῖα Καλυφώ# (ε 321, 372)
y … ἅ οἱ πόρε παρθένοc ἀδμήc# (ζ 228)
y … ὅ τοι πόρε ΦοῖβοcʼΑπόλλων# (Ο 441)
Y’ … τόν τοι πόρε πότνια μήτηρ# (Ψ 92)
Y’ … τήν οἱ πόρε ΦοῖβοcʼΑπόλλων# (Α 72, Λ 353)
Y’ … τήν οἱ πόρε δῖοc ʼΑχιλλεύc# (Ι 667) {97|98}
y … διῖ ́φιλοc||– ⏑ ⏑ – ⏓# (Κ 49, etc.)
Y’ … δουρίκλυτοc||– ⏑ ⏑ – ⏓# (Ν 210, etc.)
⏑ – ⏑ ⏑ || – ⏑ ⏑ – ⏓ (= y)
and
– – ⏑ ⏑ || – ⏑ ⏑ – ⏓ (= Y’)
respectively. Also, the word-break pattern within these shapes is simply an indirect reflex of dactylic expansion. Epithets were not inherited to fill gaps between caesura and diaeresis. They were inherited to fill out formulas. In other words, the bucolic diaeresis is motivated by the length of epithets like διΐφιλοc and δουρίκλυτοc, not vice versa.Within the metrical framework of a pher3d, both Y’ and Y formulas require a preceding x formula, while y requires X. As I have already argued, the X sector is distinct from x by virtue {98|99} of its capacity to accommodate partial (or complete) pher formulas. The only portion of the pher3d meter that cannot accommodate some kind of Pherecratic formula is sector x. Accordingly, I propose that the least traditional component of epic hexameter is to be found in the x sector. By the same token, this sector must afford the maximum opportunity for phraseological improvisation. Having just outlined such a hierarchy of XxYY’y, I should now attempt to speculate on the mechanics of composing an epic hexameter. I envisage the following set of original alternatives:
- Begin with any group of words shaped ⏓ ⏓ – ⏑ ⏑ –; continue with a formula shaped pherd, featuring initial ⏑ ⏑ instead of ⏑ –, – ⏑, – –
- Begin with a pher formula, or at least with a group of words that end with a pher formula; continue with a formula shaped ^pherd, featuring initial ⏑ instead of –
At a later stage of evolution, another alternative develops:
- Begin as in no. 1; continue with a formula shaped ^pherd, featuring initial – instead of ⏑
After the Aeolic base (⏓ ⏓) was replaced by the dactyl/spondee (– ⏔) in epic hexameter, the initial sequence x becomes identical to the Hemiepes, – ⏑ ⏑ – ⏑ ⏑ –. [62] The traditional name Hemiepes begs the question, of course, in view of the fact that dactylic hexameter is the Epos {99|100} par excellence. Still, it remains valid to claim that the elegiac pentameter,
– ⏔ – ⏔ – || – ⏑ ⏑ – ⏑ ⏑ ⏓,
did indeed originate from an acephalic/hypersyllabic Prosodiakon in distich form. [63] The strict maintenance of isosyllabism in the second part of the distich is a sure sign of archaism. Constraints here against the substitution of one long for two shorts indicate that a verse-ending is involved, not some hypothetically reapplied verse-opening. A less direct but still significant sign of archaism is the intentional practice of rhyming the last syllable before the caesura with the last syllable of the verse. [64] For example, in Theognis 174, 176, 178, 180, 182, there is a whole series of this pattern in the pentameters between the hexameters:
καὶ γήρωc πολιοῦ||Κύρνε καὶ ἠπιάλου
ῥιπτεῖν καὶ πετρέων||Κύρνε κατ’ ἠλιβάτων
οὔθ’ ἕρξαι δύναται||γλῶccα δέ οἱ δέδεται
δίζηcθαι χαλεπῆc||Κύρνε λύcιν πενίηc
ἢ ζώειν χαλεπῇ||τειρόμενον πενίῃ
In fact, such rhyme-patterns exist in one out of every seven Theognidean pentameters. The effect is to accentuate the rhythmical symmetry of the elegiac pentameter vs. the asymmetry of the epic hexameter. [65] Of course, the actual coexistence of {100|101} epic hexameter with elegiac pentameter in the framework of an elegiac couplet favors the incursion of formulas with the shape of a Hemiepes at the start of hexameter verse. To put it another way, the frequency of penthemimeral caesura in hexameter may be due partially to the influence of the obligatory caesura in pentameter.ῥιπτεῖν καὶ πετρέων||Κύρνε κατ’ ἠλιβάτων
οὔθ’ ἕρξαι δύναται||γλῶccα δέ οἱ δέδεται
δίζηcθαι χαλεπῆc||Κύρνε λύcιν πενίηc
ἢ ζώειν χαλεπῇ||τειρόμενον πενίῃ
So far, I have accounted for the following types of word-break simply by arguing for the placement of pherd and ^pherd formulas at the end of a pher3d meter:
bucolic diaeresis || – ⏑ ⏑ – ⏓
penthemimeral caesura || ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓
trochaic caesura || ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓
The bucolic diaeresis could also be caused by the placement of complete or partial pher formulas within the framework of a pherd or ^pherd. As for the hephthemimeral caesura, it could be caused by the placement of complete pher formulas, again within the framework of a pherd or ^pherd:
penthemimeral caesura || ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓
trochaic caesura || ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓
|| ⏑ ⏑ – ⏑ ⏑ – ⏓
I have yet to reckon with the trithemimeral caesura, the least significant among the major types of word-break:
|| ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓
Even here, it is possible to cite formulaic behavior for precedent. Note the existence of formulas shaped pher2d: {101|102}
… θάνατόν τε κακὸν καὶ κῆρα μέλαιναν#” (Φ 66, χ 14)
vs. formulas shaped pherd:
… θάνατον καὶ κῆρα μέλαιναν#” (β 283, etc.)
Admittedly, the shape of such a formula is pher2d from the standpoint of meter only. As we apply it to hexameter, the 2d of the symbol pher2d cannot uniformly designate two words shaped – ⏑ ⏑ any more than the d of pherd automatically designates one word shaped – ⏑ ⏑. It seems fitting to close this chapter by stressing this point once more. The principle of dactylic insertion in Pherecratics can be described as a phraseological phenomenon only on the diachronic level. So much for origins. On the synchronic level, as we observe the operative mechanics of attested Greek epic versification, dactylic insertion is a metrical phenomenon which is merely accommodated by the inherited phraseology. A formula like
… θάνατόν τε κακὸν καὶ κῆρα μέλαιναν#
represents simply the internal metrical lengthening of a formula like
… θάνατον καὶ κῆρα μέλαιναν#
Footnotes
[ back ] 1. See p. 46.
[ back ] 2. Householder and Nagy 1972:738f, 753f, 787-789 (= 1973:19, 34f, 68-70).
[ back ] 3. Allen 1966. Within the space of my summary, I cannot do justice to Allen’s argumentation, which has to be read in its entirety to be appreciated. Suffice it here to note the following: Allen uses the descriptive terms ‘pitch’ vs. ‘stress’ parallel to ‘intonation’ vs. ‘intensity’. He can cite typological parallels to the situation which he posits in Greek, i.e., intonation-systems behaving separately from intensity-systems within the same language (pp. 114f). He demonstrates decisively that high and low pitch in Greek were not correlated with high and low intensity (p. 115).
[ back ] 4. Allen 1966:123. The terms ‘heavy/light’ are the equivalent of ‘long/short’ as defined at p. 28 above.
[ back ] 5. For an attempt at refuting Allen, see the interesting article of Newton (1969). I am not prepared to answer all of Newton’s objections to Allen’s theory, although it seems fair to say that several of Newton’s ingenious arguments are not necessarily counter-arguments. For example, the fact that words shaped ⏑ – – in hexameter have ictus on the first long (Newton, p. 361) is actually to be expected if the second long is etymologically a double short. In other words, I would claim that words shaped ⏑ – – result from the precedent of earlier words shaped ⏑ – ⏑ ⏑, in terms of a diachronic viewpoint.
[ back ] 6. Cf. Meillet 1923:19, Allen 1966:118, Householder and Nagy 1972:746 (= 1973:27). See also Thompson 1961:167: “The metrical pattern imitates the structure of sound of the language; the line of the poem imitates the metrical pattern; and, therefore, the line of the poem imitates the structure of sound of the language.”
[ back ] 7. Allen 1966:119-121. In verse too, the last syllable is indifferently short/long (⏓). In, e.g., iambic patterns (… ⏓ –̣ ⏑ ⏓̣), however, the ascending rhythm imposes ictus on the last syllable. In, e.g., trochaic patterns (… –̣ ⏑ –̣ ⏓), on the other hand, the descending rhythm prevents ictus on the last syllable.
[ back ] 8. Ibid.
[ back ] 9. Allen 1966:126.
[ back ] 10. Allen 1966:128.
[ back ] 11. Allen 1966:127.
[ back ] 12. Allen 1966:126.
[ back ] 13. Cf. Snell 1962:35, Maas 1962:32.
[ back ] 14. See again pp. 46 and 49.
[ back ] 15. Kirk 1966a:76.
[ back ] 16. See Fränkel 1960 and Dale’s critique (1957:29-35); cf. also Kirk 1966:86, Ingalls 1970, 1972, Beck 1972, Beekes 1972.
[ back ] 17. Kirk 1966:90f.
[ back ] 18. Parry 1928b.
[ back ] 19. See Hainsworth 1968 passim.
[ back ] 20. Cf. especially Parry 1928b:40, 43, 57, 64.
[ back ] 21. It remains to ask why epic hexameter has no metrical irregularities shaped … – ⏑ –͎ | or … – –͎ | ⏑ – resulting from juxtaposition of formulas. In other words, why are there no instances of accidental lengthening of a short, as opposed to accidental shortening of a long? (The latter results in sequences shaped uuu. The former would have resulted in the Cretic, – ⏑ –, which is stringently avoided in the hexameter.) For a tentative answer, note that … – ⏑ –͎ | or … – –͎ | ⏑ – would reverse ictus-rhythm, whereas … ⏑ ⏑ ⏑ | only suspends it.
[ back ] 22. Hainsworth 1968:20f.
[ back ] 23. See pp. 46f.
[ back ] 24. If we substitute 1̄ 2̆ 2̆½ for 1̄̆ 2̄̆ and allow for the equation ‘two shorts equal one long’, then our pher3d schema and the sectors A/A’ and B/B’ are for the present adequate terms of description for the epic hexameter.
[ back ] 25. O’Neill 1942:60.
[ back ] 26. For the statistics, see Kirk 1966a:81f.
[ back ] 27. Cf. Hainsworth 1968:127.
[ back ] 28. Cf. Hainsworth 1968:137f.
[ back ] 29. See Householder and Nagy 1972:769f (= 1973:50).
[ back ] 30. Pp. 79f.
[ back ] 31. Cf. Hainsworth 1968:135-139.
[ back ] 32. Cf. Hainsworth 1968:137.
[ back ] 33. Cf. Hainsworth 1968:143.
[ back ] 34. Cf. Hainsworth 1968:141.
[ back ] 35. Cf. Hainsworth 1968:142f.
[ back ] 36. See pp. 37-48.
[ back ] 37. See pp. 46-48.
[ back ] 38. By O’Neill’s reckoning (1942:141).
[ back ] 39. Meister 1921:6. Even if we count enclitics like te ge per moi in the last syllable (a policy that is unjustified), the figure goes up only to 2%.
[ back ] 40. Meister 1921:6; Maas 1962:60.
[ back ] 41. Meister 1921:6; Maas 1962:60.
[ back ] 42. Cf. Maas 1962:59.
[ back ] 43. Ibid.
[ back ] 44. Meister 1921:13-22.
[ back ] 45. For grammatical implications, see Householder and Nagy 1972:783f (= 1973:63-65).
[ back ] 46. Ibid.
[ back ] 47. Hainsworth 1968:137-139.
[ back ] 48. Hainsworth 1968:143.
[ back ] 49. Hainsworth 1968:83; Hoekstra 1965:118. In some instances, one grammatical variant is older than the other (cf. especially Hoekstra, p. 117). For the most part, however, it is impossible and in fact needless to determine which of the two variants is older. The variation itself is the overarching archaic element.
[ back ] 50. Parry 1928a:54.
[ back ] 51. Parry 1928a:55-64.
[ back ] 52. Parry 1928a:54; the forms, -ᾶτο, -εῖτο, etc., are also possible.
[ back ] 53. For the common phenomenon of hiatus at the caesura, see Parry 1928b passim.
[ back ] 54. In the column at the right, I have not even counted instances where the verb in - en is followed by an overt combination of two consonants starting the next word.
[ back ] 55. Of course, I did not count these instances of πόρεν and δῶκεν as occurring before the hephthemimeral caesura in my statistics on -εν|C-. Also, the Hellenist reader might be surprised to see the particle δὲ discussed as an enclitic; but see Allen 1966:133.
[ back ] 56. See pp. 61-64, 66f.
[ back ] 57. Secondarily, it may be composed of complete pher formulas shaped UU-uu-U.
[ back ] 58. Cf. Snell 1962:36. Lobel-Page hesitate whether to adopt the variant reading εἰcέρχεται, without compelling contextual evidence. For the scansion of ἴcοc here (-u) in its original shape Ἴcvοc, see Hamm 1958:18; cf. also the scansion of epic ἶcοc (-u).
[ back ] 59. For the accusative plural -ăs and -os in Rhodian, see Bechtel II/1923:632. In line 3, the standardized orthography may conceal an underlying Καλοc + vενιαυτοc. For the possible etymology of ἐν- ‘year’ as *wen-, see Nagy 1965:311-317. Alternatively, we may wish to follow Wilamowitz (1921, p. 400) in reading καλούc τ’ ἐνιαυτούc. Note that Athenaios (8.360B) and Eustathios (Od. 1914.45) read καὶ καλοὺc ἐνιαυτούc. Page’s edition follows the precedent set by Hermann (see apparatus) in deleting the καὶ, presumably because it ruins the parallelism of καλὰc ́καλοὺc, ἐπὶ ́ἐπὶ. From this standpoint, καλούc τ’ would be an adequate emendation. Finally, I cannot determine the scansion of καλ- in καλὰc and καλοὺc (long on the basis of its original shapes Καλvανc and Καλvονc?); in any case, it occurs in a position indifferent to length.
[ back ] 60. It should be noted, however, that the ^pherd as used by Archilochos has undergone some evolution: besides ⏓ – ⏑ ⏑ – ⏑ ⏑ – ⏓, we also see ⏓ – – – ⏑ ⏑ – ⏓ (170W) and ⏑ ⏑ – ⏑ ⏑ – ⏑ ⏑ – ⏓ (if we reject West’s readings ἐρέω and φιλεῖ for ἐρέω and φιλέει at fragments 168.2 and 171W).
[ back ] 61. Parry 1928a:82.
[ back ] 62. See pp. 294f.
[ back ] 63. See pp. 294f.
[ back ] 64. For the archaism of rhyme in Greek versification, see Nagy 1972:731f.
[ back ] 65. Cf. pp. 184-189.