6. Formula and Meter: A Summary

In L’épithète traditionnelle, [1] Parry recorded his discovery that the word-break patterns of epic hexameter mark the places where formulas generally start and end. I am now prepared to add to his thesis this corollary: that the epic formulas are derived from lyric formulas appropriate mainly to Pherecratic meters. Also, I propose that the epic meter itself is derived from a lyric meter, the Pherecratic.

The Pherecratic meter is in turn derived from the Glyconic, via catalexis: If Pherecratic meters originally had their own inherited formulas, it follows that the same holds for the Glyconics. Through an intensive analysis of Sappho 44LP, a poem that is composed in a Glyconic meter (gl^2d), I have tried to show the existence of inherited Glyconic formulas which are related to but independent of the Pherecratic formulas in epic hexameter. The hexameter, which I would describe as a highly developed and sophisticated reflex of the pher^3d meter, ends with the formulas of a pher or (^)pher^d structure. [2] The more primitive Sapphic pentameter, on the other hand, ends with the {140|141} formulas of a gl structure. For example, contrast the gl shape of with the pher shape of The expression κλέοc ἄφθιτον recurs in the following (^)pher^d shape: Contrast the following plain pher shape:

In the reconstruction of a Greek pattern [4] 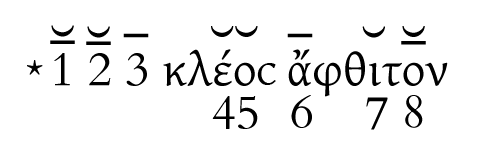and of an Indic pattern [5] 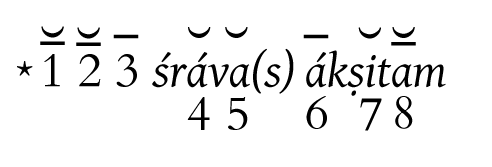we are witnessing the convergence of cognate expressions and cognate meters. In a sense, then, we have here a fragment of Indo-European versification: Unlike κλέοc ἄφθιτον, the expression κλέοc ἐcθλόν has no direct Indic equivalent. Consequently, we cannot simply assume an Indo-European origin for this combination of κλέοc, however likely it may seem. The lack of comparative evidence here is due to a characteristic development of Indic versification. Because of a general failure to preserve catalexis in dimeter, [7] there is no opportunity for any Indic cognate of κλέοc ἐcθλόν to survive.

The comparative evidence of the Indic expression śráva(s) ákṣitam shows that the formula κλέοc ἄφθιτον can be retrojected to a period so remote that it antedates the very existence of Glyconics, which I have argued to be a distinctly Hellenic development. It follows that we must seriously question any assumption that the Glyconic meter had somehow predetermined any formula such as κλέοc ἄφθιτον. The order of predetermination should be reversed. In a prehistoric period, archetypes of such expressions as κλέοc ἄφθιτον and κλέοc ἐcθλόν may have created the very precedent for the rhythms … ⏑ ⏑ – ⏑ ⏓ and … ⏑ ⏑ – ⏓ respectively.

Pursuing this hypothesis, I have examined in detail the interactions between Rig-Vedic meter and the Indic cognate of κλέοc, śrávas (Part II). I found that the positional and associative behavior of Rig-Vedic phraseology involving śrávas is highly regular even when the meter in {142|143} which it is embedded is irregular or flexible. Furthermore, the attested interchange of metrical segments from one related meter to another is matched by an interchange of traditional phraseology embedded in these segments. Although meter cannot be regular without regular traditional phraseology, traditional phraseology can be regular even without regular meter. This Rig-Vedic relationship between meter and phraseology supports my theory that traditional phraseology generated meter rather than vice versa.

In the abstract, I assume that any native poetry is regulated by the inherited constraints of a formal language which evolved from the natural language. While it evolves, of course, the formal language of poetry is being persistently matched against the esthetic or hieratic standards of both poet and audience. Formality as a social phenomenon tends toward idealization. Thus the formal language of poetry, inheriting the grammatical structure of the natural language, becomes itself an idealized structure. On a concrete level, for example, I posit that the Rig-Vedic verse evolved from an idealized grammatical phrase. The internal evidence of the Rig-Veda itself provides corroboration, in that beginnings and ends of phrases routinely correspond to the beginnings and ends of verses. [8] The main feature of the {143|144} primordial Indic verse which distinguishes it from natural phrases or clauses in the Indic language is that it must contain a fixed number of syllables. If this principle of isosyllabism arose from artificially generalizing phrases with the same number of syllables, then the principle of arranging shorts and longs in a predictable order could have arisen from artificially generalizing phrases which end in the same natural rhythm. Phrases with a favorite rhythm could be grouped together or become models for making other ideal phrases.

The formal language of poetry, although it inherits the grammatical structure of the natural language, can evolve independently of the natural language by virtue of being an idealized structure. The eventual growth of a poetic language independent of the natural language may result in different pace or direction of structural development, different regularization or obsolescence, different {144|145} mergers or splits, and so on. [9] I extend the hypothesis: any distinction between meter and phraseology grows out of the idiosyncrasies of poetic language. At first, the reasoning goes, traditional phraseology simply contains built-in rhythms. Later, the factor of tradition leads to the preference of phrases with some rhythms over phrases with other rhythms. Still later, the preferred rhythms have their own dynamics and become regulators of any incoming non-traditional phraseology. By becoming a viable structure in its own right, meter may evolve independently of traditional phraseology. Recent metrical developments may even obliterate aspects of the selfsame traditional phraseology that had engendered them, if these aspects no longer match the meter.

Let me recapitulate the specifics. The Indic evidence, where traditional phraseology can be regular even without regular meter, supports my theory that traditional phraseology had generated meter rather than vice versa. I also apply the Greek evidence to this theory. In prehistoric stages of Greek Lyric, the reasoning goes, meter was simply the built-in rhythm of the formula. From a genetic standpoint, metrical regularity stemmed from formulaic regularity. In a prehistoric period, archetypes of such formulas as κλέοc ἄφθιτον and κλέοc ἐcθλόν had created a {145|146} precedent for the rhythms … ⏑ ⏑ – ⏑ ⏓ and … ⏑ ⏑ – ⏓ respectively. Much later, these rhythms became generalized for the closing of specific meters, namely the Glyconic and Pherecratic respectively. What had once been a phraseological truncation of one syllable, such as could have become the formal prototype of metrical catalexis: In other words, I am arguing that expressions like κλέοc ἄφθιτον and κλέοc ἐcθλόν had once set the rhythmical mold for the meters in which they survive. These meters, however, have become viable entities unto themselves. As a result, the Glyconic and Pherecratic rhythms become regulators of any incoming phraseology. In comparison with Indic dimeter, the rhythmical patterns of these Greek dimeters are far more rigid and consequently more dependent on traditional phraseology.

Besides catalexis, other metrical phenomena may likewise be traced back to phraseological behavior. For example, I have argued that the system of caesuras, diaereses, and bridges in Greek epic hexameter is a reflex of the junctures where formulas start and end. The argument can be extended to the Indic meters as well, where caesuras mark the beginning or end of traditional phrases. [10] The caesura is a {146|147} synchronic metrical constant generated by a diachronic phraseological trend. For yet another example of a metrical phenomenon which can be traced back to phraseological behavior, I have adduced evidence from Homeric diction to show that the process of internal expansion originally involved the insertion of words, not of metrical units which only then had to be filled in with words. An expression with the rhythm pher could give rise to an expanded expression with the rhythm pher^d by way of inserting a word or phrase shaped – ⏑ ⏑. Of course, by the time that internal expansion survives in Greek Lyric, it has the appearance of a purely metrical process. Formations like pher^2d and pher^3d may well have resulted simply from the reapplication of such a metrical process: The number of syllables in pher^3d connotes traditional epic genre, [11] and I have proposed that it was this meter which became the well-tempered instrument of Greek epic diction, the dactylic hexameter. The pher^3d could readily accommodate a (^)pher^d formula in the closing, preceded by more flexible phraseology in the {147|148} opening. The shorter opening and the longer closing could achieve the asymmetrical effect desired in the inherited tradition of epic composition. [12]

I cannot guess how it was that some early εὑρετήc might have hit upon the pher^3d meter as a suitable vehicle for epic diction. Nor does it matter so much, perhaps. All we need remember is that the pher^3d is a distinctly Hellenic development, even if its basic elements are Indo-European in both phraseology and meter. When the dactylic hexameter finally surfaces after what must have been a considerable period of evolution, we are fortunate to find it attested in the sublime art-form of the Iliad and Odyssey. In a sense, however, we would be more fortunate if we also had attestations of earlier and more primitive epic material. I suspect that the primitive epic verses were not much different in meter from the lyric verses which we recognize as pher^3d. I also suspect that a poet like Alkaios had access to some local form of such a primitive tradition when he composed his verses in pher^3d. In any case, we may infer from the facts of Homeric diction that an immense stretch of time had already elapsed in the evolution of the hexameter. Let me recall how thoroughly the formulaic system of attested Greek Epic is pervaded by what I consider to be the following two innovations: (1) replacement {148|149} of ⏓ ⏓ by – – in the first foot, with optional substitution of – ⏑ ⏑; (2) optional replacement of – ⏑ ⏑ by – – in feet 2, 3, 4, 5. All the same, archaic elements stubbornly persist alongside the new. They abide for any analyst to see, and